NCRT math class 9th polynomial exersice 2.3

                       EXERSICE 2.3

Question 1.
Find the remainder when x3 + 3x2 + 3x + 1 is divided by
(i) x + 1
(ii) x – 
(iii) x
(iv) x + π
(v) 5 + 2x
     Solution:
     Let p(x) = x3 + 3x2 + 3x +1
(i) The zero of x + 1 is -1.
∴  p(x=-1) = (-1)^3 + 3(-1)^2 + 3(-1) +1
    = -1 + 3- 3 + 1 = 0
   Thus, the  remainder = 0

(ii) The zero of  is 

     Thus, the  remainder = 

iii) The zero of x is 0.
∴ p(0) = (0)^3 + 3(0)^2 + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
Thus, the  remainder = 1.

(iv) The zero of x + π is -π.
       p(-π) = (-π)^3 + 3(- π)^2  + 3(- π) +1
       = -π3 + 3π2 + (-3π) + 1
       = – π3 + 3π2 – 3π +1
       Thus, the required remainder is                        -π3 + 3π2 – 3π+1.

(v) The zero of 5 + 2x is  .


     Thus, the remainder is  .

Question 2.
Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Solution:
We have, p(x) = x3 – ax2 + 6x – a and zero       of x – a is a.
  ∴ p(a) = (a)3 – a(a)2 + 6(a) – a
  = a3 – a3 + 6a – a = 5a
 Thus, the  remainder is 5a.

Question 3.
Check whether 7 + 3x is a factor of 3x3+7x.
Solution:
We have, p(x) = 3x3+7x. and zero of 7 + 3x is .

Since,( ) ≠ 0
i.e. the remainder is not 0.
∴ 3x3 + 7x is not divisib1e by 7 + 3x.
Thus, 7 + 3x is not a factor of 3x3 + 7x.

NCRT CLASS 9TH MATH CHAPTER 2( POLYNOMIALS EXERSICE 2.2 SOLUTION )

              EXERSICE 2.2 

Question 1.
Find the value of the polynomial 5x – 4x2 + 3 at
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
 *    let  p(x) = 5x – 4x2 + 3
(i) so, p(x=0) = 5(0) – 4(0)2 + 3

                       = 0 – 0 + 3  =3

     Thus, p(x=o) is 3 . 

(ii) p(x=-1) = 5(-1) – 4(-1)2 + 3
                   = – 5x – 4x2 + 3 

                   = -9 + 3 = -6

     hence , the value of 5x – 4x2 + 3 at 

     x =   -1 is -6.

(iii) p(2) = 5(2) – 4(2)2 + 3 

               = 10 – 4(4) + 3
               = 10 – 16 + 3 = -3

                hence , the value of 5x – 4x2 + 3 at x = 2 is – 3.

Question 2.
Find p (0), p (1) and p (2) for each of the following polynomials.
(i) p(y) = y2 – y +1
(ii) p (t) = 2 +1 + 2t2 -t3
(iii) P (x) = x3
(iv) p (x) = (x-1) (x+1)
Solution:
(i) Given that p(y) = y2 – y + 1.

    so,
∴  P(y=0) = (0)2 – 0 + 1 = 0 – 0 + 1 = 1
    p(y=1) = (1)2 – 1 + 1 = 1 – 1 + 1 = 1
    p(Y=2) = (2)2 – 2 + 1 = 4 – 2 + 1 = 3
(ii) Given that p(t) = 2 + t + 2t2 – t3
∴ p(t=0) = 2 + 0 + 2(0)2 – (0)3

    = 2 + 0 + 0 – 0=2
   P(t=1) = 2 + 1 + 2(1)2 – (1)3
   = 2 + 1 + 2 – 1 = 4
  p(t=2) = 2 + 2 + 2(2)2 – (2)3
   = 2 + 2 + 8 – 8 = 4
(iii) Given that p(x) = x3
∴ p(x=0) = (0)3 = 0, p(1) = (1)3 = 1
    p(x=2) = (2)3 = 8
(iv) Given that p(x) = (x – 1)(x + 1)
∴ p(x=0) = (0 – 1)(0 + 1) = (-1)(1) = -1
   p(x=1) = (1 – 1)(1 +1) = (0)(2) = 0
   P(x=2) = (2 – 1)(2 + 1) = (1)(3) = 3

Question 3.

Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x) = 3x + 1,x = –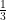
(ii) p (x) = 5x – π, x = 
(iii) p (x) = x2 – 1, x = x – 1
(iv) p (x) = (x + 1) (x – 2), x = – 1,2
(v) p (x) = x2, x = 0
(vi) p (x) = 1x + m, x = –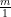 
(vii) P (x) = 3x2 – 1, x = – ,
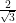
(viii) p (x) = 2x + 1, x = 
Solution:
(i) We have , p(x) = 3x + 1

(ii) We have, p(x) = 5x – π
∴ 
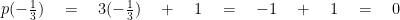
(iii) We have, p(x) = x2 – 1
∴ p(1) = (1)2 – 1 = 1 – 1=0
Since, p(1) = 0, so x = 1 is a zero of x2 -1.
Also, p(-1) = (-1)2 -1 = 1 – 1 = 0
Since p(-1) = 0, so, x = -1, is also a zero of x2 – 1.

(iv) We have, p(x) = (x + 1)(x – 2)
∴ p(-1) = (-1 +1) (-1 – 2) = (0)(- 3) = 0
Since, p(-1) = 0, so, x = -1 is a zero of (x + 1)(x – 2).
Also, p( 2) = (2 + 1)(2 – 2) = (3)(0) = 0
Since, p(2) = 0, so, x = 2 is also a zero of (x + 1)(x – 2).

(v) We have, p(x) = x2
∴ p(o) = (0)2 = 0
Since, p(0) = 0, so, x = 0 is a zero of x2.

(vi) We have, p(x) = lx + m

(vii) We have, p(x) = 3x2 – 1

(viii) We have, p(x) = 2x + 1
∴ 
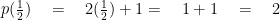
Since,  ≠ 0, so, x =  is not a zero of 2x + 1.

Question 4.
Find the zero of the polynomial in each of the following cases
(i) p(x)=x+5
(ii) p (x) = x – 5
(iii) p (x) = 2x + 5
(iv) p (x) = 3x – 2
(v) p (x) = 3x
(vi) p (x)= ax, a≠0
(vii) p (x) = cx + d, c ≠ 0 where c and d are real numbers.
Solution:
(i)  p(x) = x + 5. 

     Since, p(x) = 0
⇒ x + 5 = 0
⇒ x = -5.
    Thus, zero of x + 5 is  -5.

ii) P(x)=x - 5

    Since, p(x)=0.

     x-5=0 ⇒x=5.

     hence, zero of x - 5 is 5.

 iii)p(x) = 2x+5

      Since, p(x)=0.

      2x+5=0⇒2x=-5

       x=-5/2.

      hence zero of 2x+5 is -5/2.

iv)  p(x)= 3x-2

      Since, p(x)=0

       3x-2=0⇒x=2/3

       hence zero of 3x-2  is 2/3.

v)   p(x)= 3x

       Since, p(x)=0

       3x=0 ⇒x=0

       hence zero of 3x is 0.

vi)   p(x) =ax

        since ,p(x) =0

        ax=o ⇒x=0

         hence zero of ax is 0.

vii)  p(x)=cx+d

        since ,p(x) =0

        cx+d =0 ⇒ cx=-d

       x=-d/c

        hence zero of cx+d is -d/c

    

NCRT 9th class chapter=2 polynomials exercise 2.1

                  Exercise 2.1

Question :1)

Which of the following expressions are polynomials in one variable and which are not?

State reasons for vour answer.

 i)   4x²-3x +7

  Answer: 

      In equation 4x²-3x +7 , the one variable 'x' is given and has a power in whole number  , so the above equation is in one variable .

ii)   y²+√2

      solution 

     In equation y²+√2 , the one variable 'x' is 

      given , so the above equation is in one 

      variable .

iii) 3√t+√2 t

       Answer:

      In equation 3√t+t√2 , the power of √t =t^1/2      so the power is in fraction thats why we            can say that above expression  is not in one             variable .

iv) y+2/y

Answer :

     In equation y+2/y , the power of y is (-1).

     it is not in whole number i.e the above                 equation is not in one variable .

  

v)  x10+  y3 + t50

Answer:

     In equation x10+  y3 + t50, every variable is 

     in whole number but there is different                   variable

    (x,y,z) is given . so the above expression is          not in one variable.

 Question : 2 )

Write the coefficients of x2 in each of the following

(i) 2 + x2 + x
(ii) 2 – x2 + x3
(iii)  x2 + x
(iv) √2 x – 1
Solution:
(i)   The given polynomial is 2 + x2 + x.
       The coefficient of x2 is 1.
(ii)  The given polynomial is 2 – x2 + x3.
       The coefficient of x2 is -1.
(iii) The given polynomial is  + x.
       The coefficient of x2 is .
(iv) The given polynomial is √2 x – 1.
       The coefficient of x2 is 0.

 Question: 3.)

       Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
(i)   Abmomial of degree 35 can be                    x35 -4.
(ii)   A monomial of degree 100 can be              5x100.

Question : 4)
       Write the degree of each of the                   following polynomials.
(i) 5x3+4x2 + 7x
(ii) 4 – y2
(iii) 5t – √7
(iv) 3
Solution:
(i) The given polynomial is 5x3 + 4x2 + 7x.
The highest power of the variable x is 3.
So, the degree of the polynomial is 3.
(ii) The given polynomial is 4- y2. The highest
power of the variable y is 2.
So, the degree of the polynomial is 2.
(iii) The given polynomial is 5t – √7 . The highest power of variable t is 1. So, the degree of the polynomial is 1.
(iv) Since, 3 = 3x° [∵ x°=1]
So, the degree of the polynomial is 0.

Question 5.
Classify the following as linear, quadratic and cubic polynomials.
(i) x2+ x
(ii) x – x3
(iii) y + y2+4
(iv) 1 + x
(v) 3t
(vi) r2
(vii) 7x3
Solution:
(i) The degree of x2 + x is 2. So, it is a quadratic polynomial.
(ii) The degree of x – x3 is 3. So, it is a cubic polynomial.
(iii) The degree of y + y2 + 4 is 2. So, it is a quadratic polynomial.
(iv) The degree of 1 + x is 1. So, it is a linear polynomial.
(v) The degree of 3t is 1. So, it is a linear polynomial.
(vi) The degree of r2 is 2. So, it is a quadratic polynomial.
(vii) The degree of 7x3 is 3. So, it is a cubic polynomial.

UART communication protocol (embedded system)

What is UART?

• Universal asynchronous receiver / transmitter

• Protocol for exchanging serial data between

two devices

TX

TX

• Uses only two wires

- TX to RX (each direction)

• Can be simplex, half-duplex, or full-duplex

• Data is transmitted as frames.

Where is UART used?

• UART was one of the earliest serial protocols

Serial (COM) ports, RS-232, modems, etc.

• Popularity of UART is however decreasing:

- SPI and 12C between components

- Ethernet and USB between computers and

peripherals

• Still important for lower-speed, low-throughput

applications

About timing / synchronization

• UART is asynchronous – the transmitter and

receiver do not share a common clock

Common UART

baud rates

• The transmitter and receiver therefore must:

Transmit at the same (known) speed

- Use the same frame structure / parameters.

UART frame format:

• UART frames consist of:
• Start / stop bits
• - Data bits
• Parity bit (optional)
• • High voltage ("mark") = 1, low voltage ("space") = 0

Start and stop bits

• The start bit indicates data is coming

Transition from idle (high) to low

The stop bit(s) indicate data is complete

Stay / return to idle (high)

- Second (optional) stop bit.

Data bit :

• User (useful) data

• Length: 5 to 9 bits (usually 7 or 8)

• Data is typically sent with the least

significant bit (LSB) first.

Example:
- 7-bit ASCII 'S' (0x52) = 1 0 10011

LSB order= 110010 1

Parity bit (optional)

• Used for error detection

• Example:

ASCII 'S' (0x52 = 1010011) four 1's

- If even parity, parity bit is 0 (because

number of 1's already even)

• Even parity: number of 1's must be even

• Odd parity : number of 1's must be odd

- If odd parity, parity bit is 1 (to make the

number of 1's odd)

Summary

• UART = universal asynchronous receiver / transmitter

Simple, two-wire protocol for exchanging serial data

No shared clock – baud rate must be configured the

same on both sides

Start / stop bits used to frame user data

Optional parity bit for detecting single-bit errors

• Widely used serial data protocol, but slowly being

replaced by SPI, 12C, USB and Ethernet.

I2C bus communication protocol

I2C bus communication protocols 

What is 12c:

-Inter Integrated Circuit

-Bidirectional Data Transfer

-Half duplex (have only one data line)

-Synchronous bus so data is clocked with clock signal

-Colock is controlled when data line is changed.

Speed of 12c:

low (under 100 kbps)

Fast (400 kbps)

high speed (3.4 mbps) 12C V2.0

2 wire communication:

SDA and SCL

Vtg high = 1, low = 0.

when SLC =1, it is valid data, when SLC=0, data is changed .

Basic protocol is master slave protocol

-Master controls the clock

-Slave device may hold the clock low to prevent data transfer

-no data transfer is present when clock is low

-It is a kind of wired and connection

-need to put pullup resistor

-default it is a open-drain or open-collector, so that adding pull up resistor is necessary so that it

will have only two states that is 1.floating high and 2.drive low

-Default state is high when no device is pulling it low.

Data Transfer:

• It is byte oriented (bit)
• Ack transmited by recepient of the data
• MSB first
• First byte is address
• First byte is transmitted by master and addressed slave is the recepient
• Next byte is based on the last bit (R/ W)
• 7 bit address
• 1 bit R/ W
• 0-master write 
• First byte is transmitted by master and addressed slave is the recepient
• Next byte is based on the last bit (R/ W)
• 7bit address
• 1 bit R/ W
• 0-master write

1-master receiver.

 

Full I2C transfer:

12C Multi Master:

• It is a multi master bus
• So bus arbitration is required
• 1
• When two device tries to drive SDA to different value
• It is necessary to be sure that is not interfiering with another message
• If a device is trying to send logic one but hears logic 0, it immediately stops transmission and gives
• the other sender priority
• Synch needed in SCL

Advantages:

• Good for comm in On-board devices
• mc
• Easy to link multiple devices because of addressing scheme
• Cost and complexity do not scale up with the num of devices

Disadvantages:

The complexity of supporting software components can be higher than that of scheme (EX. SPI-No

need of address in SPI)

CBSE 10th and 12th reamaing exam 2020 and download admit card

CBSE Board Remaining Exam Date 2020

The CBSE Date Sheet 2020 or CBSE Board Exam 2020 Time Table for 10th & 12th Board exam has been released at cbse.nic.in, the official website of the Central Board Secondary Education (CBSE). As per CBSE Time Table 2020, CBSE 10th & 12th Board Exams have been started from 15th February 2020 onwards.

The complete CBSE Date Sheet for 10th and 12th Board Exam 2020 is available here for download in PDF format. Here you can learn about other important articles related to the preparation of CBSE Board Exam 2020.Cental Board of Secondary Education CBSE Board Are Finally Issued the Admit Card and Time Table, Date Sheet for the Upcoming Board Annual Examination for the High School Class 10 and Intermediate Class 12 Examination Held on February 2020. Those Candidate Are Enrolled in CBSE New Delhi Can Read the and Download Private Admit Card and Time Table.

Exam date 

Class 10th & 12th Remaining Exam : 01/07/2020 to 15/07/2020

10th and 12th cbse exam result

Class 12th Result Declared : July 2020 (Tentative)

Class 10th Result Declared : July 2020 (Tentative)

How to Download Time Table

criteria for a country to print there curency (koi country kitne note print kr sakti hai )

Can a country become rich by printing more notes? Learn the mathematics behind printing of notes

Any country usually prints notes equal to two to three percent of GDP. For this reason it is necessary to increase GDP to print more notes and to increase GDP, attention is given to factors like growth of various sectors like manufacturing and services, reducing trade deficit, etc.

Inflation may reach the peak due to printing more notes.

When asked about the well-known economist Brinda Jagirdar, he said, "We can understand this easily through the circumstances arising in Zimbabwe and Venezuela." The governmentks of these two countries printed large-scale notes for debt settlement. However, inflation rose to sky high in these two countries due to lack of economic growth, supply and demandIt is noteworthy that the African country of Zimbabwe and the South American country Venezuela printed more notes to strengthen their economy. However, the more these countries printed notes, the more the inflation increased and both these countries reached a period of 'hyperinflation'. In the year 2008, inflation in Zimbabwe registered an increase of 231,000,000%.

Model of more note printing is generally not effective


The reason behind this is that if the government or central bank will print more notes and distribute it to everyone, then everyone will have money. On the other hand, if the production of goods has stopped or there is a problem in supply, then inflation is bound to increase. According to the Jagirdar, the situation is such that even in the present circumstances, industrial production is stalled, supply is affected, there is no demand due to uncertainty, in such a situation, the government can give money in the hands of the people only to a extent.


The value of currency, sovereign rating is affected if more notes are printed.

The jagirdar said that the printing of notes over a limit reduces the value of the country's currency. Also, rating agencies reduce the country's sovereign rating. This makes it difficult for the government to get loans from other countries. Along with this, the government gets loans at high rates.

It is also important to understand this principle

Chief economist at rating agency CRISIL says that printing a small amount of rupee can help to boost economic growth, but there is a limit.

During the financial crisis of 2008, in order to strengthen the demand, almost all the central banks of the country had printed a little more money. This helped to revive demand.It was during this economic crisis that the term Quantitative Easing came into the mainstream. This means increasing the printing of notes to bring more money into people's hands. However, it was also seen that in all the countries which resorted to quantitative easing, there was devaluation of currency as well as inflation. Hence, one can say that there are more disadvantages than benefits of increasing the printing of notes.